Tutoriels Direct3D 10 : Bases

Dans le tutoriel précédent, nous avons réussi à afficher un triangle au centre de la fenêtre de notre application. Nous n'avons pas prêté beaucoup d'attention aux positions des sommets que nous avons pris dans notre vertex buffer. Dans ce tutoriel, nous allons rentrer dans le détail des positions 3D et des transformations.

L'objectif de ce tutoriel sera d'avoir un objet 3D affiché à l'écran. Là où le précédent tutoriel se concentrait sur l'affichage d'objet 2D dans un monde 3D, ici nous afficherons un objet 3D.

(SDK root)\Samples\C++\Direct3D10\Tutorials\Tutorial04

Dans le tutoriel précédent, les sommets du triangle étaient placés stratégiquement pour s'aligner parfaitement sur l'écran. Cependant, ce ne sera pas toujours le cas, et donc, nous avons besoin d'un système pour décrire les objets dans l'espace 3D et un système pour les afficher.

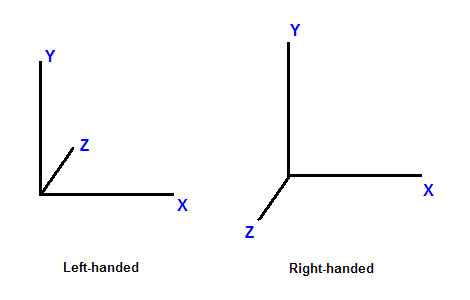
Dans le monde réel, les objets existent dans un espace 3D. Cela signifie que pour placer un objet dans une position particulière dans le monde, nous aurons besoin d'utiliser un système de coordonnées et de définir 3 coordonnées qui correspondent à la position. Dans le graphisme par ordinateur, les espaces 3D sont communément dans un système de coordonnées Cartésien. Dans ce système de coordonnées, 3 axes, X, Y, et Z, perpendiculaires les uns envers les autres, dictant les coordonnées que chaque point dans l'espace possède. Ce système de coordonnées est de plus divisé en un système main gauche et main droite. Dans un système main gauche, lorsque l'axe X pointe vers la droite et l'axe Y pointe vers le haut, et l'axe Z pointe vers l'avant. Dans un système en main droite, avec les mêmes axes X et Y, l'axe Z pointe vers l'arrière.

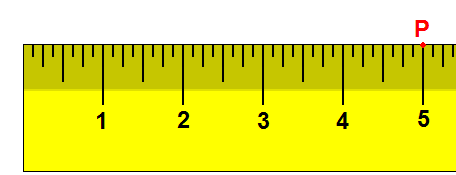
Maintenant que nous avons abordé le système de coordonnées, considérons des espaces 3D. Un point a différentes coordonnées dans différents espaces. Dans un exemple en 1D, supposons que nous ayons une règle et que nous notons le point P, à la marque 5 cm de la règle. Maintenant, si nous déplaçons la règle d'1 cm vers la droite, le même point se trouve à la marque 4 cm. En déplaçant la règle, l'image de référence a changé, et ainsi, bien que le point n'ait pas bougé, il possède une nouvelle coordonnée.

En 3D, un espace est typiquement défini par une origine et trois axes uniques depuis l'origine : X, Y et Z. Il y a plusieurs espaces habituellement utilisés dans le graphisme par ordinateur : l'espace objet, l'espace monde, l'espace vue, l'espace de projection et l'espace écran.

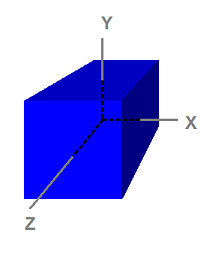
Remarquez que le cube est centré sur l'origine. L'espace objet, également appelé l'espace du modèle, correspond à l'espace utilisé par les artistes quand ils créent les modèles 3D. Habituellement, les artistes créent des modèles qui sont centrés autour de l'origine afin qu'il soit plus facile d'effectuer des transformations, telles que la rotation des modèles, comme nous le verrons quand nous nous interresserons aux transformations. Les 8 sommets ont les coordonnées suivantes :

(-1, 1, -1)
( 1, 1, -1)
(-1, -1, -1)
( 1, -1, -1)
(-1, 1, 1)
( 1, 1, 1)
(-1, -1, 1)
( 1, -1, 1)

Parce que l'espace objet est ce que les artistes utilisent habituellement quand ils dessinent et créent des modèles, les modèles qui sont stockés sur le disque sont également dans l'espace objet. Une application peut créer un vertex buffer pour représenter un tel modèle et initialiser le buffer avec les données du modèle. Ainsi, les sommets dans le vertex buffer seront habituellement aussi dans l'espace objet. Cela signifie aussi que le vertex shader reçoit en entrée les données des sommets dans l'espace objet.

L'espace Monde (World space) est un espace partagé par chaque objet dans la scène. Il est utilisé pour définir la relation spatiale entre les objets que l'on souhaite afficher (render). Pour visualiser l'espace Monde, on pourrait imaginer que nous nous trouvons dans le coin sudouest d'une pièce rectangulaire qui fait face au nord. On définit le coin où nos pieds se trouvent comme étant l'origine (0, 0, 0). L'axe X se trouve à notre droite; l'axe Y vers le haut; et l'axe Z vers l'avant, la même direction que celle dont nous faisons face. Quand on effectue ceci, chaque position dans la pièce peut être identifiée avec une série de coordonnées XYZ. Par exemple, il pourrait y avoir une chaise à 5 pieds en face et 2 pieds à notre droite. Il pourrait y avoir une lampe de 8 pieds de haut sur le plafond directement haut-dessus de la chaise. On peut se référer à la position de la chaise qui est (2, 0, 5) et la position de la lampe qui est (2, 8, 5). Comme nous pouvons le voir, l'espace monde est appelé ainsi car il nous dit où les objets sont en relation les uns les autres dans le monde.

L'espace vue, parfois appelé espace caméra, est similaire à l'espace monde en cela qu'il est typiquement utilisé pour la scène entière. Cependant, dans l'espace vue, l'origine se trouve sur le spectateur ou la caméra. La direction de la vue (où le spectateur regarde) défini l'axe Z positif. Une direction "haut" définie par l'application devient l'axe Y positif comme expliqué ci-dessous.

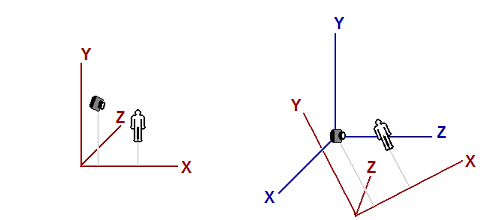
L'image de gauche montre une scène qui se compose d'un objet ressemblant à un humain et un spectateur (caméra) regardant l'objet. L'origine et les axes qui sont utilisés par l'espace monde sont indiqués en rouge. L'image de droite montre l'espace vue en relation avec l'espace monde. Les axes de l'espace vue sont indiqués en bleu. Pour éclaircir l'illustration, l'espace vue ne possède pas la même orientation que l'espace monde sur l'image de gauche pour les lecteurs. Notez que dans l'espace vue, le spectateur regarde dans la direction Z.

L'espace projection réfère à l‘espace après l'application de la transformation de projection depuis l'espace vue. Dans cet espace, le contenu visible a les coordonnées X et Y compris entre -1 et 1, et la coordonnée Z allant de 0 à 1.

L'espace écran est parfois utilisé pour se référer aux localisations dans le frame buffer. Comme le frame buffer est habituellement une texture 2D, l'espace écran est un espace 2D. Le coin supérieur gauche est l'origine avec les coordonnées (0, 0). Le X positif va vers la droite et le Y positif pointe vers le bas. Pour un tampon qui est de w pixels de large et h pixels de haut, le pixel le plus bas sur la droite a les coordonnées (w - 1, h - 1).

Les transformations sont les plus habituellement utilisées pour convertir les sommets d'un espace vers un autre. En graphisme 3D par ordinateur, il y a logiquement 3 telles transformations dans le pipeline : transformation monde, vue, et projection. Les opérations de transformations individuelles telles que la translation, la rotation, et la mise à l'échelle sont étudiées dans le tutoriel suivant.

La transformation monde, comme son nom le suggère, convertit les sommets depuis l'espace objet vers l'espace monde. Il se compose habituellement d'une ou plusieurs mise à l'échelle, rotations et translations, basées sur la taille, l'orientation et la position que nous voulons donner à l'objet. Chaque objet dans la scène possède sa propre matrice de transformation monde. C'est parce que chaque objet a sa propre taille, orientation, et position.

Après que les sommets soient convertis dans l'espace monde, la transformation vue convertit ces sommets depuis l'espace monde vers l'espace vue. En se souvenant de la conversation plus haut, disant que l'espace vue est ce que le monde paraît depuis la vue du spectateur (ou la caméra). En espace vue, le spectateur est localisé à l'origine, regardant le long de l'axe Z positif.

Il faut noter que bien que l'espace vue soit le monde depuis l'image de référence du spectateur, la matrice de transformation vue est appliquée aux sommets, pas au spectateur. D'où, la matrice de vue doit effectuer la transformation inverse que nous appliquons à notre spectateur ou caméra. Par exemple, si nous voulons déplacer la caméra de 5 unités vers la direction -Z, nous aurions besoin de calculer une matrice de vue qui déplace les sommets de 5 unités le long de la direction +Z. Bien que la caméra ait reculé, les sommets, depuis le point de vue de la caméra, ont avancé. Dans Direct3D, une API appelée D3DXMatrixLookAtLH() est souvent utilisée pour calculer une matrice de vue. Nous aurons simplement besoin de lui dire où le spectateur se trouve, où il regarde, et la direction représentant le haut du spectateur, également appelée le vecteur haut, pour obtenir une matrice de vue correspondante.

La transformation de projection convertit les sommets depuis les espaces 3D comme les espaces monde et vue vers l'espace projection. Dans l'espace projection, les coordonnées X et Y d'un sommet sont obtenues depuis les ratios X/Z et Y/Z de ce sommet dans l'espace 3D.

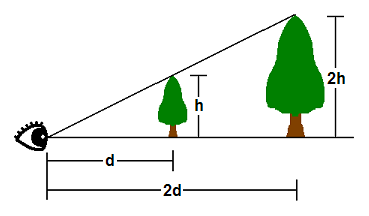
Dans l'espace 3D, les choses apparaissent en perspective. Ainsi, plus un objet est proche, plus grand il apparaît. Comme il est montré que le somemt d'un arbre à h unités de haut et à d unités de l'oeil du spectateur, apparaîtra au même point que le sommet d'un autre arbre de 2h d'unités de haut et 2d unités de distance. De cela, où un sommet apparaît sur un écran 2D est directement affecté vers ses ratios X/Z et Y/Z.

Un des paramètres qui définit un espace 3D est appelé champ de vision (field-of-view en anglais - FOV). Le FOV dénote quels objets sont visibles depuis une position particulière, pendant que l'on regarde dans une direction particulière. Les humains ont un champ de vision qui est vers l'avant (on ne peut pas voir ce qui se passe derrière nous) et on ne peut pas voir les objets qui sont trop proches ou trop loin. En graphisme par ordinateur, le champ de vision est contenu dans un frustum de vue. Le frustum de vue est défini par 6 plans en 3D. Deux de ces plans sont parallèles au plan XY. Ceux-ci sont appelés le plans Z proche et le plan Z éloigné. Les 4 autres plans sont définis par le champ de vision horizontal du spectateur et le champ de vision vertical. Le FOV le plus large est où le volume frustrum est le plus large et où le spectateur voit le plus d'objets.

Le GPU filtre les objets qui sont en dehors du frustum de vue afin qu'il n'ait pas à dépenser du temps à dessiner quelque chose qui ne sera pas affiché. Ce procédé est appelé clipping. Le frustum de vue est une pyramide à 4 côtés avec un toit découpé. Le clipping de ce volume est compliqué car pour clipper par rapport à un plan du frustrum de vue, le GPU doit comparer chaque sommet à l'équation du plan. A la place, le GPU effectue généralement d'abord la transformation de projection, et ensuite clippe sur le volume du frustrum de vue. L'effet de transformation de projection sur le frustum de vue est que la forme du frustrum de vue pyramidale devient une boîte dans l'espace projection. C'est parce que, comme mentionné plus haut, dans l'espace projection, les coordonnées X et Y sont basées sur les X/Z et Y/Z dans l'espace 3D. Donc, le point a et le point b auront la même coordonnée X et Y dans l'espace de projection, c'est pourquoi le frustum de vue devient une boîte.

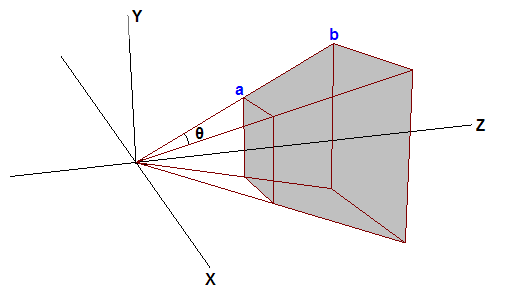
Supposez que le sommet de deux arbres se trouve exactement sur le haut une arrête du frustum de vue. De plus, supposons que d = 2h. La coordonnée Y le long de l'arrête supérieure dans l'espace projection sera ensuite 0.5 (car h/d = 0.5). Donc, les valeurs Y après projection qui sont plus grandes que 0.5 seront clippées par le GPU. Le problème ici est que 0.5 est déterminé par le champ de vision vertical choisi par le programme, et différentes valeurs de FOV produisent différentes valeurs que le GPU doit clipper à nouveau. Pour rendre le procédé plus convenable, les programmes 3D mettent généralement à l'échelle les valeurs projetées de X et Y des sommets afin que les valeurs X et Y visibles aient une portée de -1 à 1. En d'autres mots, tout ce qui a des coordonnées X et Y qui se trouvent en dehors de la portée [-1 1] sera clippé. Pour que ce schéma de clipping fonctionne, la matrice de projection doit mettre à l'échelle les coordonnées X et Y des sommets projetés par l'inverse de h/d, ou d/h. d/h est également la co-tangeante de la moitié du FOV. Avec la mise à l'échelle, le haut du view frustum devient h/d * d/h = 1. Tout ce qui est plus grand que 1 sera clippé par le GPU. C'est ce que nous voulons.

Un ajustement similaire est généralement effectué pour la coordonnée Z dans l'espace projection. On souhaiterait que le plan Z proche et le plan Z éloigné soit respectivement à 0 et 1 dans l'espace projection. Quand Z = la valeur Z proche dans l'espace 3D, Z doit être 0 dans l'espace projection; quand Z = la valeur Z éloigné dans l'espace 3D, Z doit être 1 dans l'espace projection. Après que ceci soit effectué, les valeurs Z en dehors de [0 1] seront clippées par le GPU.

Dans Direct3D 10, la manière la plus simple d'obtenir une matrice de projection est d'appeler la méthode D3DXMatrixPerspectiveFovLH(). On fournit simplement 4 paramètres-- FOVy, Aspect, Zn, et Zf -- et elle retourne une matrice qui effectue tout ce qui est nécessaire comme mentionné ci-dessus. FOVy est le FOV dans la direction Y. Aspect est le ratio d'aspect, qui est le ratio de l'espace vue de la largeur sur la hauteur. A partir de FOVy et Aspect, FOVx peut être calculé. Ce ratio d'aspect est habituellement obtenu depuis le ratio de la largeur sur la hauteur de l'affichage ciblé. Zn et Zf sont respectivement les valeurs Z proche et Z éloigné dans l'espace vue.

Dans le tutoriel précédent, nous avons écrit un programme qui affiche un seul triangle à l'écran. Quand on crée le vertex buffer, les positions des sommets que nous utilisons, sont directement dans l'espace projection afin que nous n'ayons pas à effectuer de transformation. Maintenant que nous avons une compréhension de l'espace 3D et des transformations, nous allons modifier le programme afin que le vertex buffer soit défini dans l'espace objet, comme il doit l'être. Ensuite, nous modifierons notre vertex shader pour transformer les sommets depuis l'espace objet vers l'espace projection.

Comme nous avons commencé à représenter les choses en 3 dimensions, nous avons changé le triangle plat du tutoriel précédent en un cube. Cela nous permettra de démontrer ces concepts plus clairement.

SimpleVertex vertices[] =
{
	{ D3DXVECTOR3( -1.0f, 1.0f, -1.0f ), D3DXVECTOR4( 0.0f, 0.0f, 1.0f, 0.0f ) },
	{ D3DXVECTOR3( 1.0f, 1.0f, -1.0f ), D3DXVECTOR4( 0.0f, 1.0f, 0.0f, 0.0f ) },
	{ D3DXVECTOR3( 1.0f, 1.0f, 1.0f ), D3DXVECTOR4( 0.0f, 1.0f, 1.0f, 0.0f ) },
	{ D3DXVECTOR3( -1.0f, 1.0f, 1.0f ), D3DXVECTOR4( 1.0f, 0.0f, 0.0f, 0.0f ) },
	{ D3DXVECTOR3( -1.0f, -1.0f, -1.0f ), D3DXVECTOR4( 1.0f, 0.0f, 1.0f, 0.0f ) },
	{ D3DXVECTOR3( 1.0f, -1.0f, -1.0f ), D3DXVECTOR4( 1.0f, 1.0f, 0.0f, 0.0f ) },
	{ D3DXVECTOR3( 1.0f, -1.0f, 1.0f ), D3DXVECTOR4( 1.0f, 1.0f, 1.0f, 0.0f ) },
	{ D3DXVECTOR3( -1.0f, -1.0f, 1.0f ), D3DXVECTOR4( 0.0f, 0.0f, 0.0f, 0.0f ) },
};

Si vous le remarquez, tout ce que nous avons fait est de spécifier les huit points du cube, mais nous n'avons actuellement pas décrit individuellement les triangles. Si nous avions passé ceci tel quel, la sortie ne serait pas ce que l'on attend. Nous devons spécifier les triangles qui forment le cube au travers de ces huit points.

Pour un cube, beaucoup de triangles partageront le même sommet et ce serait une perte de mémoire de les redéfinir encore et encore. Ainsi, il y a une méthode pour spécifier juste les huit points et ensuite laisser Direct3D savoir quels points prendre pour un triangle. Cela est effectué au travers d'un index buffer. Un index buffer contiendra une liste, qui réfèrera à l'indice des sommets dans le buffer, pour spécifier quels points utiliser dans chaque triangle. Le code ci-dessous montre quels points compose chacun de nos triangles.

// Créé un index buffer
DWORD indices[] =
{
	3,1,0,
	2,1,3,
	0,5,4,
	1,5,0,
	3,4,7,
	0,4,3,
	1,6,5,
	2,6,1,
	2,7,6,
	3,7,2,
	6,4,5,
	7,4,6,
};

Comme vous pouvez le voir, le premier triangle est défini par les points 3, 1, et 0. Cela signifie que le premier triangle a ses sommets respectivement à : ( -1.0f, 1.0f, 1.0f ),( 1.0f, 1.0f, -1.0f ), et ( -1.0f, 1.0f, -1.0f ). Il y a six faces pour le cube, et chaque face est composée de deux triangles, donc, vous voyez 12 triangles au total ici défini.

Comme chaque sommet est explicitement listé, et qu'aucun des deux triangles ne partage des arrêtes (au moins, de la façon dont ils ont été définis), ceci est considéré comme une liste de triangles. Au total, pour les 12 triangles dans la liste de triangle, nous devrons avoir au total 36 sommets.

La création de l'index buffer est très similaire au vertex buffer, où nous spécifions les paramètres tels que la taille et le type dans une structure, et on a appelé CreateBuffer. Le type est D3D10_BIND_INDEX_BUFFER, et comme nous avons declaré notre tableau en utilisant des DWORD, on utilisera sizeof(DWORD).

bd.Usage = D3D10_USAGE_DEFAULT;
bd.ByteWidth = sizeof( DWORD ) * 36; // 36 sommets nécessaires pour 12 triangles dans une triangle list
bd.BindFlags = D3D10_BIND_INDEX_BUFFER;
bd.CPUAccessFlags = 0;
bd.MiscFlags = 0;
InitData.pSysMem = indices;
if( FAILED( g_pd3dDevice->CreateBuffer( &bd, &InitData, &g_pIndexBuffer ) ) )
	return FALSE;

Une fois que l'on a créé ce buffer, nous devrons le définir afin que Direct3D sache se référer à cet index buffer lors de la génération des triangles. On spécifie le pointeur vers le buffer, le format, et le décalage dans le buffer pour commencer le référencement.

// Défini l'index buffer
g_pd3dDevice->IASetIndexBuffer( g_pIndexBuffer, DXGI_FORMAT_R32_UINT, 0 );

Dans notre vertex shader du tutoriel précédent, on a pris la même position d'entrée et de sortie de sommet sans aucune modification. On peut faire cela car la position d'entrée du sommet est déjà définie dans l'espace projection. Maintenant, comme la position d'entrée du sommet est définie dans l'espace objet, nous devons la transformer avant de la sortir du vertex shader. On effectue ceci en 3 étapes : on transforme depuis l'espace objet vers l'espace monde, on transforme de l'espace monde vers l'espace vue, et on transforme de l'espace vue vers l'espace projection. La première chose que nous devons faire est de déclarer 3 variables de buffer constants. Les buffers constants sont utilisés pour stocker des données que l'application a besoin de passer aux shaders. Avant l'affichage, l'application écrit habituellement des données importantes dans les buffers constants, et ensuite durant l'affichage, les données peuvent être lues depuis l'intérieur des shaders. Dans un fichier FX, des variables de buffer constants sont déclarées comme des variables globales en C++. Les 3 variables que nous utiliserons sont les matrices de transformation monde, vue et projection de type HLSL "matrix".

Une fois que nous avons déclaré les matrices dont nous aurons besoin, on met à jour notre vertex shader pour transformer la position d'entrée en utilisant les matrices. Un vecteur est transformé en multipliant le vecteur par une matrice. Dans HLSL, ceci est effectué en utilisant la fonction intrinsèque mul(). Notre déclaration de variable et le nouveau vertex shader sont montrés ci-dessous :

matrix World;
matrix View;
matrix Projection;
//
// Vertex Shader
//
VS_OUTPUT VS( float4 Pos : POSITION, float4 Color : COLOR )
{
	VS_OUTPUT output = (VS_OUTPUT)0;
	output.Pos = mul( Pos, World );
	output.Pos = mul( output.Pos, View );
	output.Pos = mul( output.Pos, Projection );
	output.Color = Color;
	return output;
}

Dans le vertex shader, chaque mul() applique une transformation à la position d'entrée. Les transformations monde, vue, projection sont appliquées dans cet ordre séquentiellement. Ceci est nécessaire car la multiplication de vecteurs et de matrices n'est pas commutative.

Nous avons mis à jour notre vertex shader pour transformer en utilisant les matrices, mais nous avons aussi besoin de définir 3 matrices dans notre programme. Ces trois matrices stockeront la transformation pour être utilisées lors de l'affichage. Avant l'affichage, on copie les valeurs de ces matrices dans le buffer constant de shader. Ensuite, quand on débute l'affichage en appelant Draw(), notre vertex shader lit les matrices stockées dans le buffer constant. En plus des matrices, nous avons aussi besoin de définir 3 pointeurs ID3D10EffectMatrixVariable. ID3D10EffectMatrixVariable est un objet qui représente une matrice dans le buffer constant. Nous pouvons utiliser ces 3 objets pour copier les matrices vers le buffer constant. Ainsi, nos variables globales possèdent ceci en plus :

ID3D10EffectMatrixVariable* g_pWorldVariable = NULL;
ID3D10EffectMatrixVariable* g_pViewVariable = NULL;
ID3D10EffectMatrixVariable* g_pProjectionVariable = NULL;
D3DXMATRIX g_World;
D3DXMATRIX g_View;
D3DXMATRIX g_Projection;

Pour initialiser les 3 objets ID3D10EffectMatrixVariable, on appelle ID3D10Effect::GetVariableByName() après la création de l'effet, en passant le nom de la variable qui nous intéresse. GetVariableByName() retourne une interface ID3D10EffectVariable, même si l'objet sous-jacent est spécifique au type de variable définie dans le fichier FX. Dans ce cas, les objets sous jacents sont ID3D10EffectMatrixVariable. Pour obtenir une interface ID3D10EffectMatrixVariable depuis un ID3D10EffectVariable, on peut appeler sa méthode AsMatrix() :

g_pWorldVariable = g_pEffect->GetVariableByName( "World" )->AsMatrix();
g_pViewVariable = g_pEffect->GetVariableByName( "View" )->AsMatrix();
g_pProjectionVariable = g_pEffect->GetVariableByName( "Projection" )->AsMatrix();

La chose suivante que nous avons besoin de faire est de pointer avec les 3 matrices que nous utiliserons pour faire la transformation. Nous voulons que le triangle soit à l'origine, parallèle au plan XY. Voici exactement comment cela est stocké dans le vertex buffer dans l'espace objet. Ainsi, la transformation monde ne doit rien faire, et nous initialisons la matrice monde avec une matrice identité. Nous souhaitons configurer notre caméra afin qu'elle soit située à [0 1 -5], regardant au point [0 1 0]. On peut appeler D3DXMatrixLookAtLH() pour calculer correctement une matrice de vue pour nous en utilisant le vecteur haut [0 1 0] car nous souhaitons toujours que la direction Y+ reste toujours vers le haut. Finalement, pour avoir une matrice de projection, on appelle D3DXMatrixPerspectiveFovLH(), avec un FOV vertical de 90 degrés (pi/2), un ratio d'aspect de 640/480 qui apporte la taille de notre back buffer, et les Z proche et éloigné respectivement à 0.1 et 100. Cela signifie que tout ce qui est plus proche que 0.1 ou plus loin que 100 ne sera pas visible à l'écran. Ces trois matrices sont stockées dans les variables globales g_World, g_View, et g_Projection.

Nous avons les matrices, et maintenant nous devons les écrire dans le buffer constant quand nous dessinons afin que le GPU puisse les lire. Les buffers constants sont étudiés en profondeur dans le prochain tutoriel. Pour l'instant, considérez-les comme les conteneurs pour les constantes passées aux shaders. Car nous écrivons les matrices dans le buffer constant, on appelle la méthode de SetMatrix() de ID3D10EffectMatrixVariable, en lui passant la matrice à écrire dans le buffer. Ceci doit être effectué avant que l'on fasse l'appel à Draw().

//
// Met à jour les variables
//
g_pWorldVariable->SetMatrix( (float*)&g_World );
g_pViewVariable->SetMatrix( (float*)&g_View );
g_pProjectionVariable->SetMatrix( (float*)&g_Projection );