Tutoriels Direct3D 10 : Bases

Dans le tutoriel précédent, on a dessiné un cube depuis l'espace modèle à l'écran. Dans ce tutoriel, nous allons étendre le concept de transformation et montrer une simple animation qui peut être faite avec ces transformations.

Au final de ce tutoriel, nous aurons un objet qui tourne autour d'un autre. Il sera utile de décrire les transformations et comment elles peuvent être combinées pour obtenir l'effet désiré. Les tutoriaux futurs seront construits sur cette fondation quand nous introduirons de nouveaux concepts.

(SDK root)\Samples\C++\Direct3D10\Tutorials\Tutorial05

En graphisme 3D, la transformation est souvent utilisée pour opérer sur des sommets et des vecteurs. C'est aussi utilisé pour les convertir d'un espace vers un autre. La transformation est effectuée via multiplication avec une matrice. Il y a typiquement 3 types de transformation primitive qui peuvent être effectuées sur des sommets : la translation, la rotation , et le scaling (sa distance depuis l'origine). En plus de celles-ci, la transformation de projection est utilisée pour passer de l'espace vue à l'espace projection. La bibliothèque D3DX contient des API qui peuvent construire commodément une matrice pour beaucoup de buts tels que la translation, la rotation, le scaling, la transformation monde vers vue, la transformation vue vers projection, etc. Une application peut ensuite utiliser ces matrices pour transformer les sommets dans sa scène. Une compréhension basique des transformations de matrices est nécessaire. On va brièvement examiner ci-dessous quelques exemples.

La translation se réfère au mouvement ou déplacement d'une certaine distance dans l'espace. En 3D, la matrice utilisée pour la translation a la forme :

    1  0  0  0
    0  1  0  0
    0  0  1  0
    a  b  c  1

Où (a, b, c) est le vecteur qui définit la direction et la distance de déplacement. Par exemple, pour déplacer un sommet de -5 unités le long de l'axe X (direction X négative), on peut la multiplier avec cette matrice :

    1  0  0  0
    0  1  0  0
    0  0  1  0
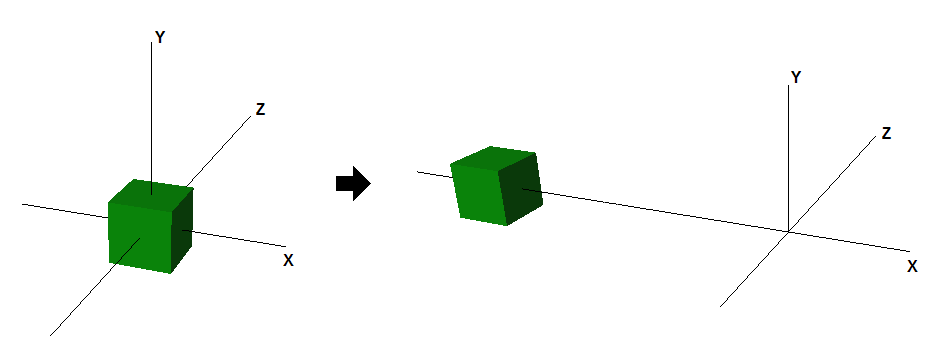
   -5  0  0  1

Si nous appliquons ceci à un objet cube centré à l'origine, le résultat est que la boîte est déplacée de 5 unités vers l'avant sur l'axe X négatif, comme indiqué sur la figure 1, après que la translation soit appliquée.

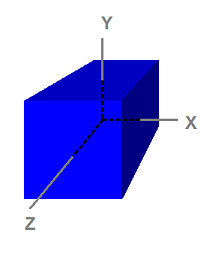
En 3D, un espace est typiquement défini par un point d'origine et trois axes uniques depuis l'origine : X, Y et Z. Il y a plusieurs espaces habituellement utilisés en graphisme sur ordinateur : l'espace objet, l'espace monde, l'espace vue, l'espace projection et l'espace écran.

La rotation se réfère à la rotation des sommets sur un axe en partant de l'origine. Ces 3 axes sont les axes X, Y, et Z dans l'espace. Un exemple en 2D ferait pivoter le vecteur [1 0] de 90 degrés dans le sens contraire des aiguilles d'une montre. Le résultat de la rotation est le vecteur [0 1]. La matrice utilisée pour la rotation ? dans le sens des aiguilles d'une montre sur l'axe Y ressemble à ceci :

    cos?  0   -sin?  0
     0    1     0    0
    sin?  0    cos?  0
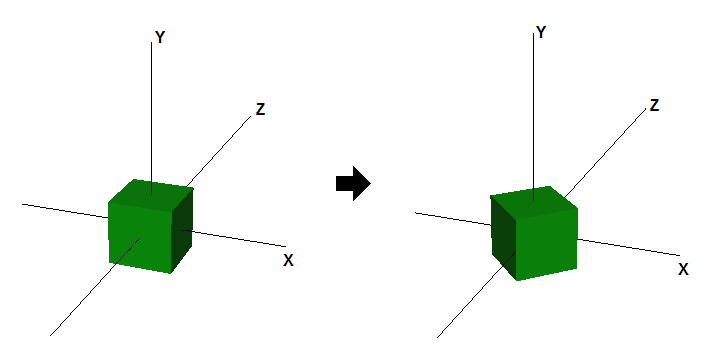
     0    0     0    1

La figure 3 montre l'effet de rotation d'un cube, centrée à l'origine, de 45 degrés sur l'axe Y.

Le scaling se réfère à l'agrandissement ou la diminution de la taille de vecteurs composants le long des axes. Par exemple, un vecteur peut être agrandi dans toutes les directions ou réduit seulement sur l'axe X. Pour faire le scaling, on applique habituellement la matrice ci-dessous :

    p  0  0  0
    0  q  0  0
    0  0  r  0
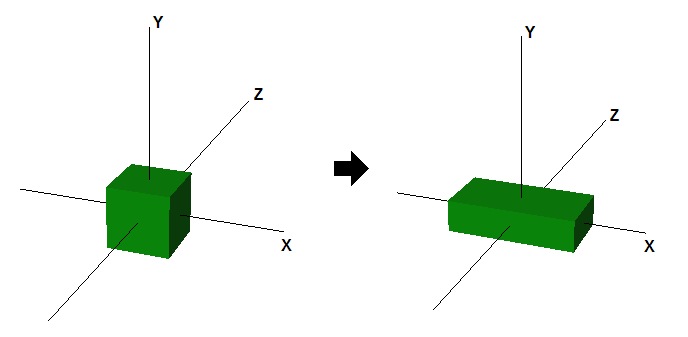
    0  0  0  1

Où p, q, et r sont les facteurs de scaling le long des directions X, Y et Z, respectivement. La figure 4 montre l'effet de scaling par 2 le long de l'axe X et le scaling par 0.5 le long de l'axe Y.

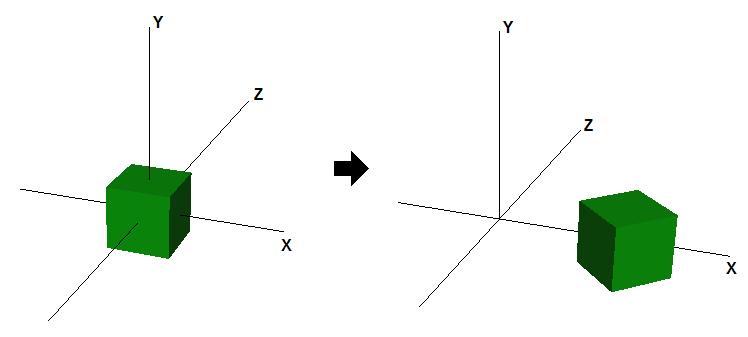
Pour appliquer de multiples transformations à un vecteur, on peut simplement multiplier le vecteur par la première matrice de transformation et, ensuite, multiplier le vecteur résultant par la seconde matrice de transformation, et ainsi de suite. La multiplication des vecteurs et des matrices étant associative, on peut aussi multiplier toutes les matrices d'abord et ensuite multiplier les vecteurs par la matrice du produit et obtenir un résultat identique. La figure 5 montre comment le cube serait si nous combinions ensemble une rotation et une translation.

Dans ce tutoriel, on va transformer deux cubes. Le premier tournera sur place, pendant que le second tournera autour du premier, et tournera sur son propre axe. Les deux cubes auront leur propre matrice de transformation de monde qui leur est associée, et cette matrice leur sera réappliquée à chaque frame dessinée.

Il y a des fonctions dans D3DX qui nous assisterons dans la création de la matrice de rotation, de translation et de scaling.

• Les rotations effectuées autour des axes X, Y et Z sont accomplies avec les fonctions D3DXMatrixRotationX, D3DXMatrixRotationY, et D3DXMatrixRotationZ respectivement. Elles créent des matrices de rotations basiques qui tournent autour des axes primaires. Les rotations complexes autour d'autres axes peuvent être effectuées en multipliant ensemble plusieurs d'entre elles.
• Les translations peuvent être effectuées en invoquant la fonction D3DXMatrixTranslation. Cette fonction créera une matrice qui va translater les points spécifiés par les paramètres.
• Le scaling est effectué avec D3DXMatrixScaling. Elle fait le scaling seulement le long des axes primaires. Si le scaling le long d'axes arbitraires est souhaité, alors la matrice de scaling peut être multipliée avec une matrice de rotation appropriée pour accomplir l'effet.

Le premier cube tournera sur place et agira comme le centre de l'orbite. Le cube a une rotation le long de l'axe Y appliquée à la matrice monde associée. C'est effectué en appelant la fonction D3DXMatrixRotationY montrée ci-dessous. Le cube est pivoté par un certain montant à chaque frame. Comme les cubes sont supposés tourner continuellement, la valeur par laquelle la matrice de rotation est basée est incrémentée avec chaque frame.

    // 1er Cube : tourne autour de l'origine
    D3DXMatrixRotationY( &g_World1, t );

Le second cube orbitera autour du premier. Pour montrer de multiples transformations, un facteur de scaling, et son propre axe de rotation seront ajoutés. La formule utilisée est montrée juste en dessous du code (en commentaire). D'abord le cube sera réduit à l'échelle d'une taille de 30%, et ensuite sera pivoté autour de son propre axe de rotation (l'axe Z dans ce cas). Pour simuler l'orbite, il sera translaté depuis l'origine, et ensuite, pivoté autour de l'axe Y. L'effet désiré peut être obtenu en utilisant 4 matrices séparées avec leur transformation individuelle (mScale, mSpin, mTranslate, mOrbit), puis, multipliées ensemble.

    // 2ème Cube : tourne autour de l'origine
    D3DXMATRIX mTranslate;
    D3DXMATRIX mOrbit;
    D3DXMATRIX mSpin;
    D3DXMATRIX mScale;
    D3DXMatrixRotationZ( &mSpin, -t );
    D3DXMatrixRotationY( &mOrbit, -t*2.0f );
    D3DXMatrixTranslation( &mTranslate, -4.0f, 0.0f, 0.0f );
    D3DXMatrixScaling( &mScale, 0.3f, 0.3f, 0.3f );

    D3DXMatrixMultiply( &g_World2, &mScale, &mSpin );
    D3DXMatrixMultiply( &g_World2, &g_World2, &mTranslate );
    D3DXMatrixMultiply( &g_World2, &g_World2, &mOrbit );
    //g_World2 = mScale * mSpin * mTranslate * mOrbit;

Un point important à noter est que ces opérations ne sont pas commutatives. L'ordre dans lequel les transformations sont appliquées est important. Expérimentez avec l'ordre de transformation et observez les résultats.

Comme toutes les fonctions de transformation vont créer une nouvelle matrice depuis les paramètres, le montant avec lequel elles pivotent doit être incrémenté. Ceci est effectué en mettant à jour la variable "time".

    // Met à jour le temps (time)
    t += D3DX_PI * 0.0125f;

Avant que les appels d'affichage ne soient effectués, la technique doit collecter les variables pour les shaders. Ici, la matrice monde, la matrice vue et la matrice de projection sont attribuées vers la technique. Notez que la matrice monde est propre à chaque cube, et donc, change pour chaque objet qui passe par elle/lui.

    //
    // Affiche le 1er cube
    //
    D3D10_TECHNIQUE_DESC techDesc;
    g_pTechnique->GetDesc( &techDesc );
    for( UINT p = 0; p < techDesc.Passes; ++p )
    {
        g_pTechnique->GetPassByIndex( p )->Apply(0);
        g_pd3dDevice->DrawIndexed( 36, 0, 0 );
    }

    //
    // Met à jour les variables pour le second cube
    //
    g_pWorldVariable->SetMatrix( (float*)&g_World2 );
    g_pViewVariable->SetMatrix( (float*)&g_View );
    g_pProjectionVariable->SetMatrix( (float*)&g_Projection );

    //
    // Affiche le second cube
    //
    for( UINT p = 0; p < techDesc.Passes; ++p )
    {
        g_pTechnique->GetPassByIndex( p )->Apply(0);
        g_pd3dDevice->DrawIndexed( 36, 0, 0 );
    }

Il y a un ajout important dans ce tutoriel, qui est le buffer de profondeur (depth buffer). Sans lui, le cube le plus petit en orbite serait toujours dessiné au dessus du cube plus grand au centre quand il se trouverait à l'arrière du dernier. Le buffer de profondeur permet à Direct3D de garder des traces de la profondeur de chaque pixel dessiné à l'écran. Le comportement par défaut du buffer de profondeur dans Direct3D 10 est de vérifier chaque pixel dessiné à l'écran par rapport à la valeur stockée dans le buffer de profondeur pour ce pixel dans l'espace écran. Si la profondeur du pixel affiché est moindre ou égale à la valeur déjà dans le buffer de profondeur, le pixel est dessiné et la valeur dans le buffer de profondeur est mise à jour par la profondeur du pixel nouvellement dessiné. D'autre part, si le pixel dessiné a une profondeur plus grande que la valeur déjà dans le buffer de profondeur, le pixel est ignoré et la valeur de profondeur dans le buffer de profondeur reste inchangée.

Le code suivant dans l'exemple crée un buffer de profondeur (une texture DepthStencil). Il crée aussi une DepthStencilView du buffer de profondeur afin que Direct3D 10 sache l'utiliser en tant que texture Depth Stencil.

    // Crée une texture depth stencil
    D3D10_TEXTURE2D_DESC descDepth;
    descDepth.Width = width;
    descDepth.Height = height;
    descDepth.MipLevels = 1;
    descDepth.ArraySize = 1;
    descDepth.Format = DXGI_FORMAT_D32_FLOAT;
    descDepth.SampleDesc.Count = 1;
    descDepth.SampleDesc.Quality = 0;
    descDepth.Usage = D3D10_USAGE_DEFAULT;
    descDepth.BindFlags = D3D10_BIND_DEPTH_STENCIL;
    descDepth.CPUAccessFlags = 0;
    descDepth.MiscFlags = 0;
    hr = g_pd3dDevice->CreateTexture2D( &descDepth, NULL, &g_pDepthStencil );
    if( FAILED(hr) )
        return hr;

    // Crée la depth stencil view
    D3D10_DEPTH_STENCIL_VIEW_DESC descDSV;
    descDSV.Format = descDepth.Format;
    descDSV.ViewDimension = D3D10_DSV_DIMENSION_TEXTURE2D;
    descDSV.Texture2D.MipSlice = 0;
    hr = g_pd3dDevice->CreateDepthStencilView( g_pDepthStencil, &descDSV, &g_pDepthStencilView );
    if( FAILED(hr) )
        return hr;

Afin d'utiliser ce buffer depth stencil nouvellement créé, le tutoriel doit l'attribuer au device. C'est effectué en passant la vue depth stencil au troisième paramètre de la fonction OMSetRenderTargets.

    g_pd3dDevice->OMSetRenderTargets( 1, &g_pRenderTargetView, g_pDepthStencilView );

Comme avec la cible affichée, nous devons aussi vider le buffer de profondeur avant l'affichage. Cela assure que les valeurs de profondeur des frames précédentes n'ignorent pas incorrectement les pixels dans la frame actuelle. Dans ces tutoriaux le buffer de profondeur est configuré pour avoir un nombre maximum de (1.0).

    //
    // Vide le depth buffer à 1.0 (profondeur max)
    //
    g_pd3dDevice->ClearDepthStencilView( g_pDepthStencilView, D3D10_CLEAR_DEPTH, 1.0f, 0 );